10205. Highways
The island nation of
Flatopia is perfectly flat. Unfortunately, Flatopia has a very poor system of
public highways. The Flatopian government is aware of this problem and has
already constructed a number of highways connecting some of the most important
towns. However, there are still some towns that you can't reach via a highway.
It is necessary to build more highways so that it will be possible to drive
between any pair of towns without leaving the highway system.
Flatopian towns are numbered
from 1 to n and town i has a position given by the Cartesian
coordinates (xi, yi). Each highway connects
exactly two towns. All highways (both the original ones and the ones that are
to be built) follow straight lines, and thus their length is equal to Cartesian
distance between towns. All highways can be used in both directions. Highways
can freely cross each other, but a driver can only switch between highways at a
town that is located at the end of both highways.
The Flatopian government
wants to minimize the cost of building new highways. However, they want to
guarantee that every town is highway-reachable from every other town. Since
Flatopia is so flat, the cost of a highway is always proportional to its
length. Thus, the least expensive highway system will be the one that minimizes
the total highways length.
Input. The first line contains the
number of test cases. Then there’s a blank line and the datasets separated by a
blank line. Each test case consists of two parts. The first part describes all
towns in the country, and the second part describes all of the highways that
have already been built.
The first line of the test
case contains the number of towns n (1 ≤ n ≤ 750). Each of the next n lines
contains two integers xi and yi – the coordinates of the i-th
town (for i from 1 to n). The absolute value of coordinates is
no more than 10000. Every town has a unique location.
The next line contains the
number of existing highways m (0 ≤
m ≤ 1000). Each of the next m lines contains a pair of town numbers
which are already connected by a highway. Each pair of towns is connected by at
most one highway.
Output. For each test case print a
single line for each new highway that should be built in order to connect all
towns with minimal possible total length of new highways. Each highway should
be presented by printing town numbers that this highway connects, separated by
a space.
If no new highways need to
be built (all towns are already connected), then print the sentence “No
new highways need”.
Print a blank line between
test cases.
|
Sample input |
Sample output |
|
1 7 3 3 6 2 8 1 6 0 2 0 0 1 0 3 3 4 2 5 2 6 7 |
1 7 6 5 2 3 |
SOLUTION
graphs – Prim
algorithm
Algorithm analysis
Let us single out the connected components
by the already existing connections, using the system of disjoint sets. Run
Prim’s algorithm. If an edge that connects vertices from one connected
component is relaxed, consider its length equal to zero. While adding an edge
to MST, unite the vertices at its ends into one set.
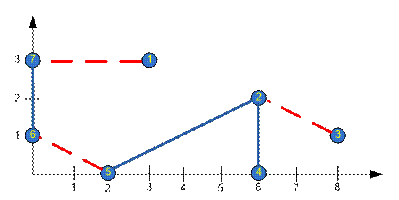
Example
Consider the sample given. Already built highways are
marked in blue. Highways to be built are given in red.
Algorithm realization
Declare the
arrays. Store the city coordinates in (x[i], y[i]). The value used[i] = 1, if vertex i is included in MST. The dist[i]
value stores the smallest distance from a vertex not yet included in MST to the
current MST. The prev[i] value
contains a vertex from MST, to which it would be better to connect vertex i. When the vertex i is included to MST, then the edge (prev[i], i) belongs to MST.
#define MAX 751
#define INF 0x3F3F3F3F
int mas[MAX], x[MAX], y[MAX], used[MAX], dist[MAX], prev[MAX];
Function Repr returns the representative of the vertex n.
int Repr(int n)
{
if (n == mas[n]) return n;
return mas[n] = Repr(mas[n]);
}
Function Union unites the sets that contain vertices x and y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
mas[x] = y;
return (x != y);
}
The function dist2 computes the squared distance between
cities i and j.
int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
Function Prim implements the Prim’s
algorithm
void Prim(void)
{
Initialize the arrays.
memset(dist, 0x3F, sizeof(dist));
memset(used, 0, sizeof(used));
memset(prev, -1, sizeof(prev));
Start to construct the MST from the vertex 1. Initialize dist[1] = 0, used[1] = 1.
int i, j, cur = 1;
dist[cur] = 0;
used[cur] = 1;
Make n – 1 iterations. At each iteration, add one vertex
to MST (so n – 1 vertices should be added
to MST).
for (i = 1; i <
n; i++)
{
The current vertex is cur. Iterate over the edges (cur, j) and recalculate the
value of dist[j]. Thus dist[j] stores the current shortest
distance from vertex j to the current MST.
for (j = 1; j <= n; j++)
{
if (!used[j])
{
If the vertices cur
and j lie in the same connected
component, then the distance between them set to 0 (dist[j] =
0).
if (Repr(cur) ==
Repr(j))
{
dist[j] = 0;
prev[j] = cur;
}
else if (dist2(cur, j)
< dist[j])
{
dist[j] =
dist2(cur, j);
prev[j] = cur;
}
}
}
Find the shortest edge that
will be included in MST. To do this, look for the smallest dist[j]
such that the vertex j does not yet belong to MST (used[j] = 0). The number of the vertex with the smallest
dist[j] is stored into cur (it
becomes the current one).
int min = INF;
cur = -1;
for (j = 1; j <=
n; j++)
if (!used[j]
&& (dist[j] < min))
{
min = dist[j];
cur = j;
}
Vertex cur is included to MST. The edge (prev[cur], cur)
is added to MST.
used[cur] = 1;
If the
vertices cur and prev[cur] are
not connected with roads yet, construct a road (prev[cur],
cur). Unite the sets that
contain vertices cur and prev[cur].
if (Repr(cur) !=
Repr(prev[cur]))
{
printf("%d
%d\n", prev[cur], cur);
Union(prev[cur],
cur);
}
}
}
The main
part of the program. Process tests tests.
scanf("%d", &tests);
while (tests--)
{
Read the
input data.
scanf("%d", &n);
for (i = 1; i <= n; i++)
scanf("%d %d", &x[i],
&y[i]);
Initialze
the system of disjoint sets.
for (i = 1; i <= n; i++) mas[i] = i;
scanf("%d", &m);
For each
edge (u, v) unite the sets that
contain vertices u and v. In the variable cnt compute the number of edges used for their union.
cnt = 0;
for (i = 0; i < m; i++)
{
scanf("%d %d", &u,
&v);
cnt += Union(u, v);
}
If cnt = n – 1, then the initially existing highways form a connected graph. There
is no need to build new highways.
if (cnt == n - 1)
puts("No new highways need");
else
Prim();
Print the
empty line between the tests.
if (tests) puts("");
}